In der Datenanalyse gibt es drei zentrale Kennzahlen, die oft verwendet werden, um den zentralen Wert einer Datenmenge zu beschreiben: Modus, Mittelwert und Median. Obwohl sie auf den ersten Blick ähnlich wirken, liefern sie unterschiedliche Informationen über die Daten. In diesem Beitrag erfährst du, wie sie sich unterscheiden, wann du welche Kennzahl einsetzen solltest und bekommst ein leicht verständliches Beispiel.
1. Mittelwert (Durchschnitt)
Der arithmetische Mittelwert wird berechnet, indem man alle Werte summiert und durch die Anzahl der Werte teilt.
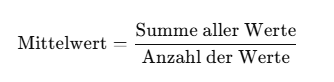
Beispiel:
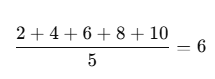
✅ Gut geeignet, wenn die Daten keine extremen Ausreißer enthalten.
❌ Nachteil: Stark anfällig für Ausreißer (z. B. ein extrem hoher Wert verfälscht das Ergebnis).
2. Median (Zentralwert)
Der Median ist der Wert, der die Daten in zwei gleich große Hälften teilt, wenn sie der Größe nach sortiert sind.
Beispiel:
Die Werte sind: 2, 4, 6, 8, 100
Median = 6 (der mittlere Wert in der sortierten Liste)
✅ Vorteil: Weniger anfällig für Ausreißer als der Mittelwert.
❌ Nachteil: Berücksichtigt nicht die genaue Verteilung der anderen Werte.
3. Modus (häufigster Wert)
Der Modus ist der Wert, der am häufigsten in einer Datenmenge vorkommt.
Beispiel:
Die Werte sind: 2, 4, 4, 6, 8
Modus = 4 (weil die 4 am häufigsten vorkommt)
✅ Besonders nützlich, wenn man die häufigste Kategorie oder den populärsten Wert ermitteln möchte (z. B. häufigste Schuhgröße).
❌ Nachteil: Es kann mehrere Modi geben oder keinen, wenn alle Werte gleich oft vorkommen.
📊 Anschauliches Beispiel mit allen drei Werten
| Daten | 2 | 4 | 4 | 6 | 100 |
|---|---|---|---|---|---|
| Mittelwert | → 23,2 | ||||
| Median | → 4 | ||||
| Modus | → 4 |
👉 Hier siehst du, wie ein Ausreißer (100) den Mittelwert nach oben zieht, während Median und Modus den „typischen“ Wert besser abbilden.
Wann verwendet man welche Kennzahl?
- Mittelwert: Bei normal verteilten Daten ohne Ausreißer
- Median: Bei verzerrten Daten oder Ausreißern
- Modus: Bei kategorischen Daten oder um den häufigsten Wert zu bestimmen
🔗 Fazit
Das Verständnis von Modus, Mittelwert und Median ist essenziell, um Daten richtig zu interpretieren. In der Praxis sollten Analysten oft mehrere dieser Kennzahlen berechnen, um ein vollständiges Bild zu erhalten.
