Die Z-Standardisierung, auch bekannt als Z-Score-Normalisierung, ist eine der wichtigsten Techniken in der Datenanalyse und Statistik. Sie ermöglicht es, Datenpunkte aus unterschiedlichen Skalen vergleichbar zu machen – ein entscheidender Schritt, wenn du mit Daten aus verschiedenen Quellen arbeitest.
Was ist Z-Standardisierung?
Z-Standardisierung bedeutet, dass du jeden Wert einer Datenreihe so umrechnest, dass die gesamte Reihe einen Mittelwert von 0 und eine Standardabweichung von 1 hat.
Dadurch kannst du Daten unabhängig von ihrer ursprünglichen Einheit (z. B. Euro, Kilogramm, Sekunden) direkt miteinander vergleichen.
Die Formel lautet:
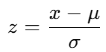
- xxx = Wert, den du standardisieren möchtest
- μ = Mittelwert der Daten
- σ = Standardabweichung der Daten
Warum ist das wichtig?
Stell dir vor, du möchtest die Leistungen von zwei Sportlern vergleichen:
- Sportler A läuft 100 Meter in 10,2 Sekunden
- Sportler B springt 2,10 Meter hoch
Ohne Standardisierung kannst du diese Werte nicht direkt vergleichen.
Mit Z-Standardisierung kannst du aber herausfinden, wer im Verhältnis zu seiner Disziplin besser abschneidet.
Einfaches Beispiel mit Excel
Du hast folgende Daten (Körpergröße in cm):
| Person | Größe |
|---|---|
| A | 180 |
| B | 170 |
| C | 190 |
| D | 175 |
| E | 185 |
- Berechne den Mittelwert (μ):
μ=(180+170+190+175+185)/5=180
- Berechne die Standardabweichung (σ):
σ≈7,9
- Berechne den Z-Wert für Person B (170 cm):
z=(170−180)/7,9≈−1,27z
Interpretation: Person B ist 1,27 Standardabweichungen kleiner als der Durchschnitt.
Grafische Darstellung
Du kannst die Verteilung in Excel oder Python einfach visualisieren:
- Excel: Erstelle ein Histogramm der Größen, markiere den Mittelwert und zeichne die Z-Werte als Abweichungen ein.
- Python (Matplotlib):
pythonCopyEditimport numpy as np
import matplotlib.pyplot as plt
data = [180, 170, 190, 175, 185]
mean = np.mean(data)
std = np.std(data)
z_scores = [(x - mean) / std for x in data]
plt.bar(['A','B','C','D','E'], z_scores, color='steelblue')
plt.axhline(0, color='red', linestyle='--')
plt.title("Z-Standardisierung der Körpergrößen")
plt.ylabel("Z-Score")
plt.show()
Diese Grafik zeigt auf einen Blick, wer über oder unter dem Durchschnitt liegt.
Wann solltest du Z-Standardisierung anwenden?
- Bei Machine Learning, wenn Features unterschiedliche Skalen haben
- Bei Vergleichen von Messwerten aus verschiedenen Einheiten
- In der Finanzanalyse, um Renditen verschiedener Aktien zu vergleichen
- Bei Anomalieerkennung, um Ausreißer zu identifizieren
Fazit
Die Z-Standardisierung ist ein einfaches, aber extrem mächtiges Werkzeug. Sie macht Daten vergleichbar und sorgt dafür, dass deine Analysen korrekte und aussagekräftige Ergebnisse liefern.
